ABSTRACT:
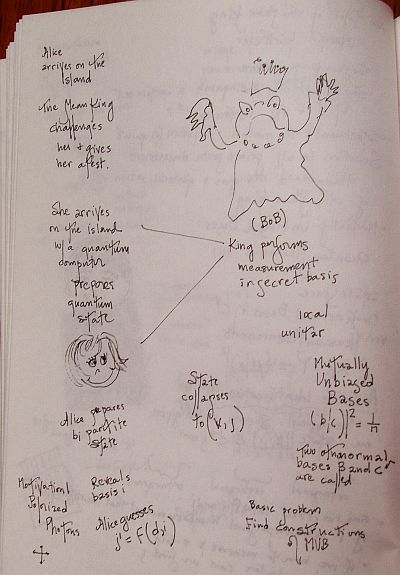
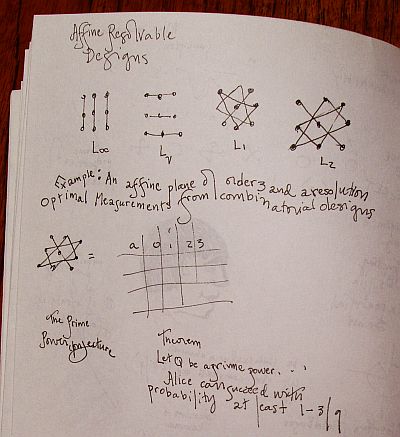
The Mean King's problem asks to predict the outcome of a measurement which is randomly selected from a set of mutually complementary observables. The challenge is to make this prediction right away without actually knowing the observable, i.e., the information which observable was chosen is revealed only later in time. I will review this problem and offer a combinatorial solution which works whenever the system's dimension is a power of a prime number. More generally, I will show that whenever an affine resolvable design exists, then a state reconstruction problem similar to the Mean King's problem can be defined and solved. As an application of this general framework we consider a state reconstruction problem which can be solved using Hadamard designs. Using a different approach we show that if the dimension of the system is large, the measurement result in the Mean King's problem as well as the secretly chosen measurement basis can be inferred with high probability. This can be achieved even when the mean-spirited King is unwilling to reveal the measurement basis at any point in time.